简介

随着机器人变得日益成熟，它们已经能够应用到处理越来越多的工业工序。6自由度（6Dof）机器人能够执行复杂的动作，因而可以在许多复杂的工业任务当中展示良好的性能，比如码垛、搬运、涂胶和焊接等。6自由度机器人可以提举和灵活地操纵重型载荷，并通过复杂的几何运动对载荷进行精确操控。

基于其良好的性能和灵活性，6自由度机器人被用来与各种工具相结合，应用于许多不同的任务。但是，每次引入新的工具时，都需要进行精确的重新校准，然后才能发挥这种机器人的能力。重新校准经常既耗费时间又不准确，妨碍了工业过程的顺利运作，对生产造成拖延。

Servotronix创造了一种有效的位置示教方法，可以对6自由度机器人所使用的新工具进行快速校准，并且不必依赖制造商测量或外部传感器。该方法简单、准确，对实际应用非常有效。

校准

6自由度机器人执行任务时需要对工具进行保持和移动。为了达到令人满意的性能，机器人在工作时必须知道工具的精确位置。每次装配不同工具时，机器人都必须再次精确地校准。

校准6自由度机器人有不同的方法。比如与参考部件接触，使用距离传感器，以及使用激光干涉仪测量等。此外，可以将外部传感器，比如摄影系统，装在机器人的不同位置，以便获取机器人校准参照物体的精确位置。

这些方法既耗费时间，又比较复杂。Servotronix开发了一款更加简单的方法，并且已经实现了卓越的结果。以下我们将对该方法加以说明。

确定工具中心点

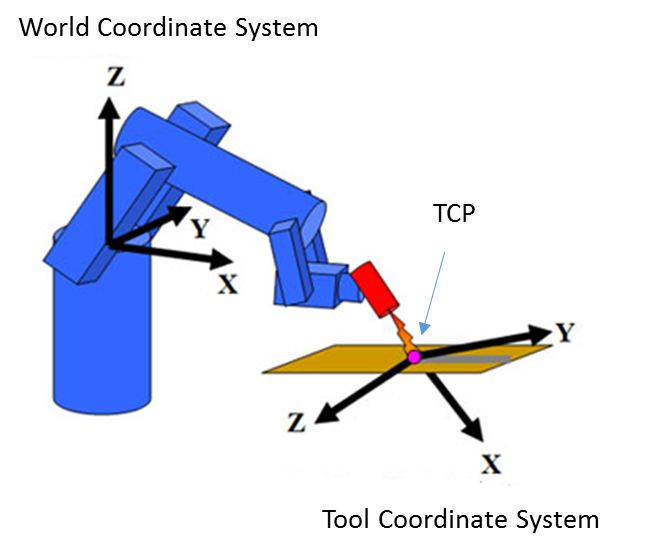
我们使用运动学校准方法来确定工具中心点（TCP），所有机器人定位都是以该点为基准加以定义。TCP定义在世界坐标系下 – 可对世界上的任何一点进行定位的笛卡尔坐标系统 。该坐标系统相对于所述机器人将始终保持静止。

工具坐标系

工具坐标系定义了工具的位置和姿态，并且将坐标的零点设在工具的中心点（TCP）。机器人的TCP将会随着其执行笛卡尔运动而移动到已编程位置。更换工具将会改变工具的坐标系，因此需要重新校准，以便使新的TCP准确到达目标位置。

在许多机器人应用当中，TCP的运动轨迹意味着机器人工作空间内的复杂路径，通常为一条变姿态的工具直线路径。此工具本身需要偶尔更换，甚至需要频繁更换。每次更换工具时，在机器人恢复操作之前，必须确定并配置一组新的几何参数。

在大多数工业应用当中，对于机器人任务编程来说，位置示教是最实用的方法。使用这种方法时，必须具备高精度的工具参数（通常来自制造商），包括工具的角偏移（偏航，俯仰和翻滚）以及笛卡尔偏移，以便生成具有可控的工具姿态的直线路径。

但不幸的是，操作者经常会发现工具的几何参数识别会受到某些制约，比如说：（1）没有来自制造商关于工具尺寸的资料；（2）没有可用的硬件协助；（3）无法得知如何将工具安装到机器人法兰。在面临这些限制时，每次更换工具，操作者都必须浪费大量时间去校准工具。

精确评估简化标定

Servotronix已经开发出一种方法，用于快速和精确地估算工具几何参数，无需外部传感器、视觉或其他协助，也无需拆卸工具。在这种位置示教方法当中，操作者只需将6自由度机器人的TCP放在几个不同的位姿，然后自动输入Servotronix的工具尺寸评估算法。该算法可以快速确定新工具的精确校准参数，从而使工具快速投入使用。

这种校准方法的精度将会随着工具位姿样本的增加而提高。我们的实验表明，使用逆齐次转换矩阵未必能够生成期望的结果，但使用最小二乘法将可产生精确的校准值。

Servotronix的方法

我们使用一个配有工具的6自由度机器人，六个Servotronix高性能CDHD伺服驱动器，以及Servotronix softMC控制器进行测试。我们的方法只涉及分析计算而无需拆卸工具。我们只评估XYZ尺寸，并且假设工具的端点处于恒定的笛卡尔坐标位置。

不证自明的是，所有指向同一位置的机器人姿态必须位于一个球体上，并且工具端点位于球体中心：

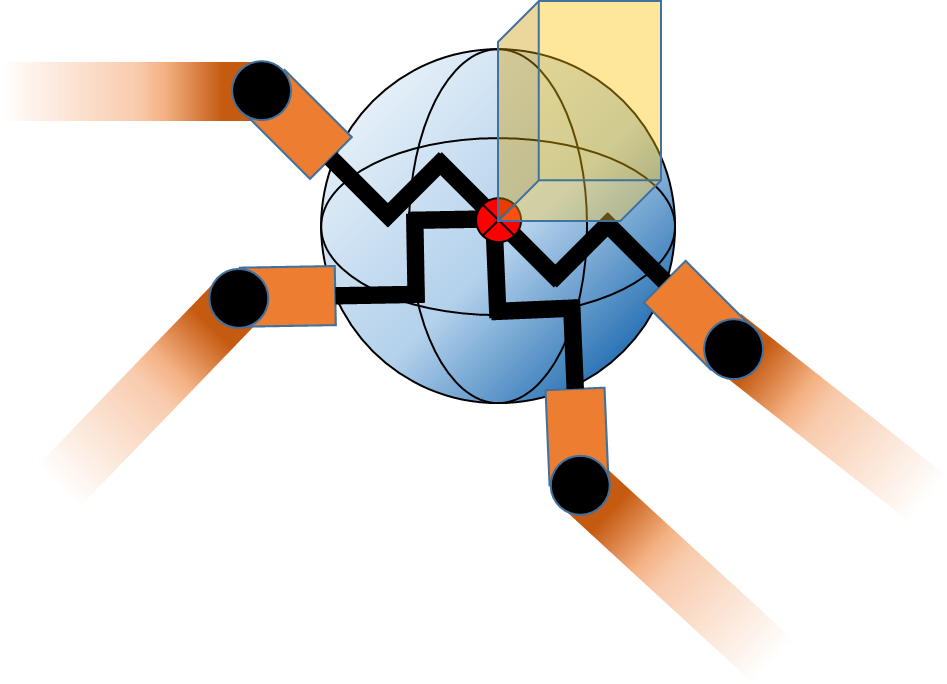
通过对球体上的点进行测量，即可计算TCP。

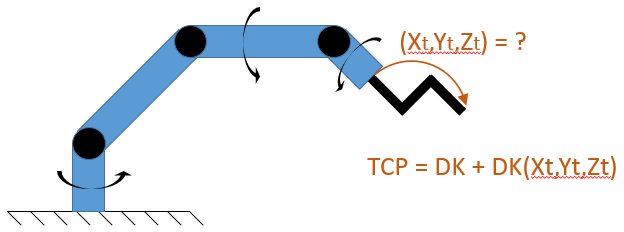
其中t代表中心

R2 = (X - Xt)2 + (Y - Yt)2 + (Z – Zt)2

在方程（1）当中有四个未知参数（R，Xt，Yt，Zt）。X，Y，以及Z值是通过运动学正解加以计算。为了实现可接受的精度，我们的方法要求至少使用四个点来定义一个球体。因此，四个这样的设置将是：

R2 = (X1 - Xt)2 + (Y1 - Yt)2 + (Z1 – Zt)2

R2 = (X2 - Xt)2 + (Y2 - Yt)2 + (Z2 – Zt)2

R2 = (X3 - Xt)2 + (Y3 - Yt)2 + (Z3 – Zt)2          

R2 = (X4 - Xt)2 + (Y4 - Yt)2 + (Z4 – Zt)2

通过使用方程减法，我们不仅可以消除未知变量R，并且可以清除方程中的所有非线性组分。这将会生成一组1次多项式方程，可以通过最小二乘法拟合进行求解。如果采用的点多于4个，将会产生更多的方程和更高的精度。

这种按部就班的方法仅需几分钟时间即可完成，共需进行至少四次测量，如下所示：

总结

Servotronix的方法快速、准确、经济，可以无需拆卸工具进行校准。该方法无需专用硬件，可以节省新工具安装所需的时间和精力。机器制造商可以很方便地使用这种方法，对6自由度机器人的工具进行快速、精确和几乎无成本的再校准，从而增强机器人在广泛应用中的操作平稳性，加快生产速度。