数控木工加工中心伺服驱动系统仿真设计

0 引言

　　目前，仿真技术往往被用于在设计之后进行模拟试验，其实也可用于复杂系统的设计求解。采用PID控制的控制器设计，为兼顾快速性和稳定性，其控制参数较难确定，而且依靠软硬件实现都比较麻烦。由于进给伺服系统趋于数字化，即控制方法采用时间离散型采样控制，控制器可采用差分模型，先找出系统输入输出的一些关系，再用仿真的方法来反求控制器的各系数，这也是一种有效的设计方法。

1 控制器数学模型的建立

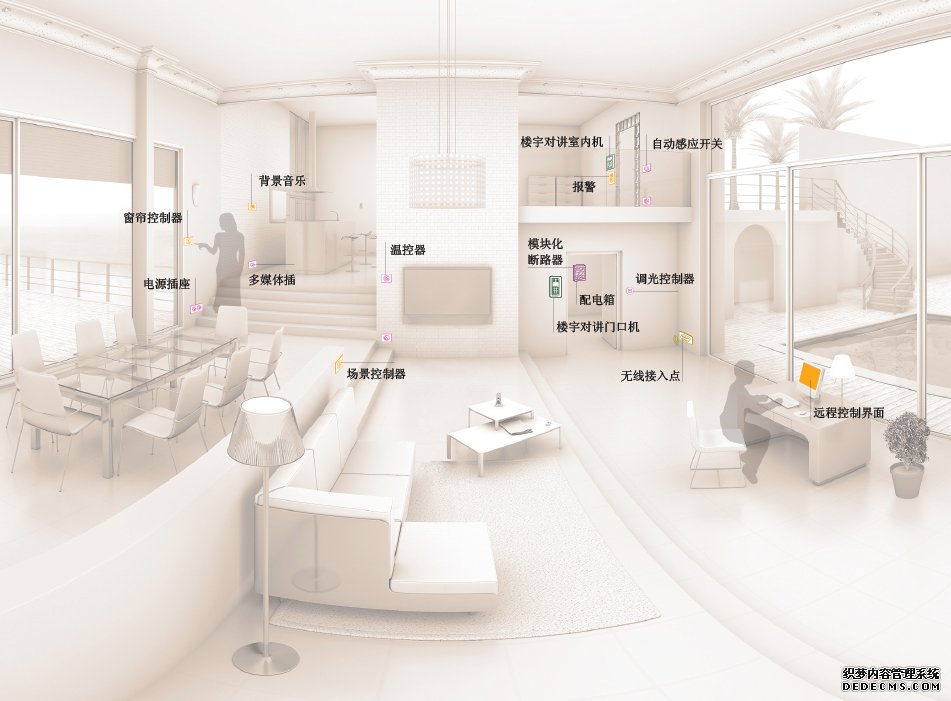
　　建立控制器数学模型，PID控制器的传递函数为:

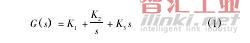
　　PID控制器的框图见图1。

　　上述公式是线性常系数差分方程组，以此作为控制器的数学模型方便计算机控制系统的实现。差分方程控制器D(Z)模型见图2。

2 伺服驱动系统数学模型的建立

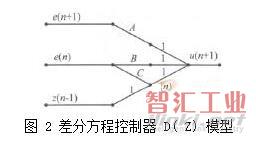
　　根据数控木工加工中心进给速度要求高，而加工精度要求相对低一点的特点，采用半闭环伺服系统和数字控制方式。将伺服进给系统分成机械传动机构和伺服驱动系统。设计要求为进给速度为15m/min，脉冲当量为0.01mm。选择电动机:MDDDT5540，额定功率为1kW，最高转速为3000r/min，增量编码器为10000p/r，丝杠螺距为5mm。为简化结构，只设位置环，不设速度环。伺服驱动系统框图见图3。

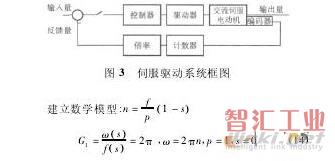
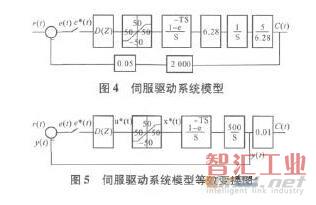
　　交流伺服电动机，增量编码器G2=10000P/5mm=2000P/mm，倍率G4=1/(2000×0.01)=0.05。驱动器:一部分为零阶保持器，一部分为限幅器，计数器G3=1。控制器:D(Z)。伺服驱动系统模型见图4，等效变换见图5。

3 伺服驱动系统仿真设计

　　加入非线性环节的系统进行仿真的方法:分别求取差分方程控制器的差分方程与连续部分的脉冲传递函数的差分方程，在每一个响应时刻分别对两部分进行一次计算，插入非线性环节，连接输入输出，以得到控制器下一时刻的输入。控制器差分方程:

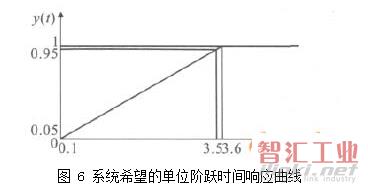
　　饱和非线性环节:当u(n)≥50时，x(n)=50;当－50≤u(n)≤50时，x(n)=u(n);当u(n)≤－50时，x(n)=－50。连接方程:e(n)=r(n－1)－y(n－1)。如果仿真也像神经网络法一样去进行训练是行不通的，一是太多的样本难以获得，二是计算量太大。其实只要找出系统的输入输出在趋于稳定状态时的关系，仿真求出满足关系的一组控制器方程组系数即可。根据系统的稳定性、快速性、准确性要求确定输出响应。伺服驱动系统在v=15m/min，脉冲当量为0.01mm，y(t)=1时，稳态时间应在4×10－5之内。时间在0～10－6s，系统加速;时间在10－6～3.5×10－5s，系统匀速，以最高速度运动;时间在3.5×10－5s～3.6×10－5s，系统减速;时间在3.6×10－5s～4.0×10－5s，系统趋于稳定并达到稳态值。系统希望的单位阶跃时间响应曲线见图6，

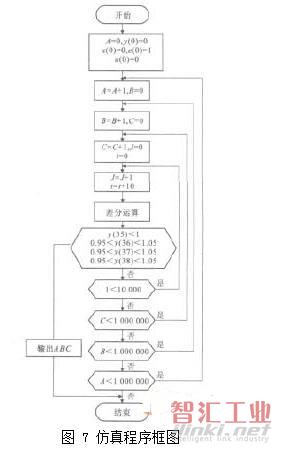
　　伺服驱动系统输入最高频率为25000Hz，反馈最高频率为50000Hz，根据采样定理，取采样频率为106Hz，采样周期T=10－6s。当r(t)=1时，控制y(35)，y(36)，y(37)和y(38)等的值，通过仿真反求出一组满足条件的系数ABC。仿真程序框图见图7。

　　仿真结果:A=431500，B=25200和C=500，将求得的ABC值带入数学模型，再次仿真，取T=10－6s，n=100，求解得输出响应见图8。仿真结果:调整时间为4.0×10－5s，输出误差在±0.05之内。换算成进给速度为15m/min，正好达到设计要求。

4 结论

　　伺服驱动系统控制器的设计采用差分方程组作模型简单可行，只要将控制器的设计和系统的设计融为一体，建立各部分的差分模型，找出系统输入输出在趋于稳定状态时的关系，仿真求出满足关系的一组控制器差分方程组系数即可，而该模型又方便在数字伺服驱动系统中靠软件实现。