1 引 言
数控编程是目前 CAD/CAPP/CAM 系统中最能发挥效益的环节之一,其在实现设计加工自动化、提高加工精度和加工质量、缩短产品研制周期等方面发挥着重要作用。针对模具电极加工的数控自动编程系统的研究已取得不少成果,然而在半精加工的处理上效果不甚理想,大大制约了数控加工自动化程度的提高。
数控铣削中,为了提高加工效率、降低加工成本,首先用大刀快速粗加工。为了获得零件准确形状、精确的尺寸和良好的表面质量,往往要用合适的刀具进行精加工。高效率的粗加工后要获得高精度的精加工,合理地安排半精加工至关重要。研究半精加工的特征识别,减少自动编程系统的人机交互,对模具制造的效率提升具有重要意义。因此提出一种利用截面法获得模型的截面线形状并通过对截面线形状的分析来识别半精加工特征的算法。
2 半精加工特征识别
在精加工之前,为了去除由于粗加工刀具直径较大或转角半径大而遗留的材料,使精加工时零件的加工余量较小且较为均匀而进行的加工称为半精加工。是否需要半精加工操作,取决于粗加工刀具尺寸和待加工零件(以下简称模型)的形状。例如粗加工刀具为D10,是否需要半精加工要看待加工模型是否存在粗加工刀具D10加工不到的方,若存在8 mm宽的凹槽则需要半精加工。数控加工中半精加工特征的识别实质上是识别刀具无法到达的内R角、凹槽以及孔洞。综上所述,半精加工特征识别转化为模型的凹槽、孔洞最小尺寸Dmin以及内R角的最小尺寸Rmin的识别。半精加工特征识别算法的具体流程如图1所示,该算法主要由三部分组成:轮廓的获取、轮廓的表达和参数的识别。下面具体介绍关键算法。
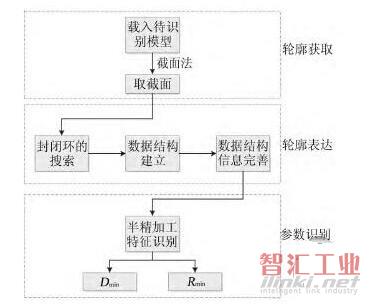
图1 半精加工特征识别算法流程
2.1 截面轮廓的获取
待加工模型的加工坐标系确定后,模型的凹槽或内R角是以顺着Z轴负方向的视线看到的模型轮廓内凹的部分,因而截面方向选为Z轴正向。截面数量的选取如图2所示。模型由2个台阶面组成(台阶面和基准面),在每个台阶顶面上抬0.01 mm的高度做截面(目的是避免截面位于临界处,导致截面的形状无法确定),截面数量取决于模型的平面的数量。采用该方法确定截面数量是保证获得的截面轮廓能够遍历到模型所有的内R角和凹槽的前提下的最少数目。
算法步骤:
(1)统计模型在基准面以上(包含基准面)的电极头部包含的所有水平面,沿Z轴正向从低到高作面的排序,用一个有序数组an记面的对应的Z轴坐标,同一高度面的高度值记一次。
(2)将数组an的每一项值加0.01mm。分别以an的每一项数值为高度,Z轴正向为截面法向,对模型作截面,得到截平面与模型轮廓形成的交线。图2所示模型包含2个台阶面:基准面和台阶面,获得的截面轮廓如图3所示。
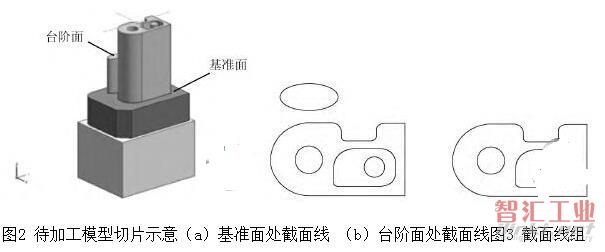
2.2 截面线轮廓的表达
为了便于对截面线轮廓进行分析,需要设计合适的数据结构表达截面线轮廓。主要需要表达各元素的几何信息,各几何元素之间的相对位置关系,各个直(曲)线之间的连接关系等。
作截面获得的构成轮廓的各曲线段tag(句柄)数组是随机无序排列的,为了将二维轮廓用数据结构形式表达出来,需要对该曲线段数组进行处理,用封闭轮廓搜索算法将这些实体按照构成封闭环归类,并且形成有向、顺序排列tag数组。将组成轮廓的曲线段集进行封闭轮廓搜索分类后,再建立对应的链表数据结构来表达截面轮廓。表达截面轮廓的数据结构如图4所示。
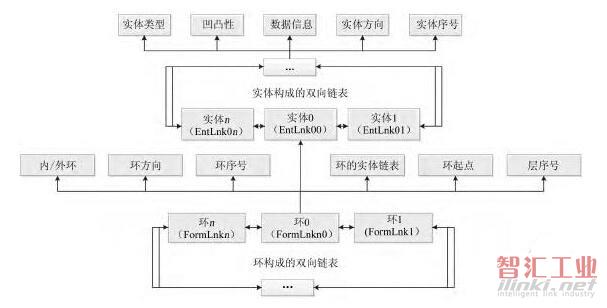
图4 表达截面轮廓的数据结构
截面轮廓按图4链表数据结构框架搭建完成后,需要计算其几何属性,如环的方向、内外环判断、轮廓节点凹凸性等,具体算法如下:
(1)环方向判别。环方向的判断是通过计算环的面积是正值还是负值来确定环的方向,简称求面积法。
(2)内外环的判断。对于任意一个外环的所有内环中,有可能是外环的一级内嵌、二级内嵌,甚至有几个内嵌的环,在半精加工的特征识别时需要区分内外环主要目的是判断轮廓的凹凸性,为了便于分析,将轮廓按嵌套关系标上层号,即最外层的外
轮廓层号为0,其一级内嵌层号为1,二级内嵌环层号为2……,处于偶数层的环定义为外环,位于奇数层的环则为内环,有了以上的定义后,则可介绍判断内外环的算法。以图3中基准面处截面线轮廓为例,环L1没有内环,环L2镶嵌内环L3和L4,同时环L4又镶嵌环L5,关系较为复杂,如图5所示。
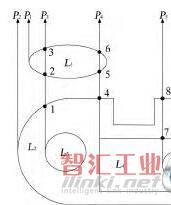
图5 轮廓的多环关系及其射线P
1~ P5的分布环关系树建立过程为:①过环i的最左点作Y轴正向平行且同向的射线;②计算该射线和其他各环交点的Y坐标,并记录交点所在的环;③将所有交点按照Y坐标值的大小(从小到大)进行排序;④删除与射线相交次数为偶数的环的全部交点;⑤若没有一个交点,则环i没有父环;若有交点,则Y坐标值最小的交点所在的环即为环i的父环。在实现该步骤过程中,可能含有大量短直线和小曲线的环划分为严格的单调链和平行单调链。在求射线与环交点过程中,当射线刚好通过两条单调链的交点时,需要作特别设定:(a)两条单调链同时位于射线左侧,按零交点处理;(b)两条单调链位于射线两侧,按照一个交点处理;(c)两条单调链同时位于射线右侧,按照2个交点处理;⑥从左至右考察各环,依据
环与其父环建立环关系树,如图6所示。环关系树构建完成后,通过环所属的层值可以判断内外环,关系树的层值设置如图7所示。位于偶数层的环为外环,位于奇数层的环为内环,图7中L1、L2、L4为外环,根据内外环的几何关系,图7中的阴影部分即为模型的截面。

图6 环关系树的构建过程示意图 图7 环关系树的层值设置以及截面
(3)轮廓节点处的凹凸性判断。在上述轮廓线中取一外轮廓(见图8),要求确定节点A处的凹凸性,算法为:①在A点邻域内,分别在构成点A的2个实体上取点B和C;②在A、B、C三点沿轮廓的方向排序,构成三角形△CAB;③计算三角形△CAB的面积;④判断面积的符号,如为正,则节点A为凸节点,否则为凹节点。
对于顺时针方向的轮廓,其结论与上述结果相反;对内环轮廓,其结论又与外轮廓的情况相反。
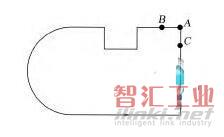
图8 轮廓的凹凸性判断
利用上述算法分析轮廓数据结构中所有节点的凹凸性,若构成A点的2个实体为直线,则B、C取直线的另一个端点,若实体为非直线,将实体等弧长分割简化成多段小直线,从而方便用直线的方式来处理,分析出其凹凸性。
至此表达截面线轮廓的数据结构构建全部完成。
2.3 特征参数的识别
截面线轮廓的特征参数包括侧面最小内R角半径Rmin和最小槽间距值Dmin。识别出这些特征值便能确定使用何种尺寸刀具能够完成加工,进而确定相应的加工工艺,具体识别算法如下。
2.3.1 侧面最小内 R 角
截面轮廓被表达为由多个环按所处层号联系在一起的数据结构,侧面内R角的分析针对单个环进行,由于环的几何形状变化较多,需要分如下3种情况讨论。
(1)内环由整圆或者封闭圆锥曲线单个实体组成。整个内环都为内凹的,内R角半径值为圆的半径或者椭圆的半短轴,如图9(a)中R1和R2所示。
(2)构成环的实体中有样条曲线时。样条曲线的凹凸性并不一定是单调的,为了简化分析,把样条曲线按等弧长分成小段曲线并且将小段曲线的凹凸性近似看作单调的。这样,样条曲线的内R角计算需分段进行,当小曲线段为内凹时,获取样条曲线在该段范围内的最小曲率半径作为此小曲线段的内R半径值,综合比较组成样条曲线的所有曲线段的内R半径,取最小值作为该样条曲线的内R半径值。小段曲线的凹凸性采用选择曲线段的中点,求其凹凸性代表曲线段整体的凹凸性的方法进行判断。
图9(b)所示的一个轮廓外环,环的方向为顺时针,曲线AD为样条曲线,首先将样条曲线按弧长等分为两段,增加等分点E,经过等分操作,此时构成轮廓环的各实体都是凹凸性单调的。直线的凹凸性用直线起点的凹凸性代替,判断构成该轮廓环的所有实体的凹凸性,结果是曲线段ED为内凹,其他实体为外凸的,最后求出曲线 ED 的最小半径值Rmin,即为该轮廓环的最小内R半径值。
(3)构成环的实体中的开放圆弧或者开放圆锥曲线。根据几何特性圆弧与圆锥曲线凹凸性都是单调的,因而不需要像样条曲线一样作等分操作,取曲线段中点的凹凸性代替曲线段的凹凸性,其他判断过程同样条曲线的做法类似。图9(c)所示圆弧EF为内凹的,其他实体均为外凸的,则圆弧段的半径R即为整个环的最小内R半径值Rmin。
2.3.2 最小槽间距 Dmin
在数控编程的方案中,是否需要半精加工以及操作所用刀具需要分析待加工模型的凹槽与间隙的尺寸,以保证选用的刀具可以深入到凹槽或间隙中进行加工。为分析方便,将凹槽与间隙的尺寸一并归为槽间距。待加工电极的形状较多,给槽间距做一个大致的分类便于后续分析。
2.3.2.1 凹槽的分类
(1)位于环关系树零层的外环之间形成的间隙。最外层环与其他最外层环之间两两求得最小距离,确切地说是间隙值,这是槽间距的第一种类型
(2)内环与其子环之间形成的间隙。在环关系树中若位于奇数层的内环存在子环,则此内环与子环共同构成一段环状间隙,这是槽间距的第二种类型,如图11所示。槽间距值为内环与其子环的最小距离Dmin。
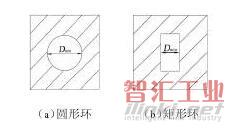
图11 内环与其下一级内嵌外环构成的凹槽
(3)环关系树最高层的内环形成的凹槽。位于环关系树最高层的内环在模型中为凹槽或孔洞的截面形状,因为内环的形状变化较多,综合来说有3种典型的情况,如图12所示。对于这3种情况的槽间距取值分别标志在图12中,特别是图12(c)所示的环形状为三角形时,槽间距值取3条边中最短边对应的中位线的长度。
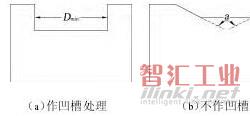
(a)圆形环 (b)矩形环 (c)三角形环图12 环关系树最高层内环自身形成的凹槽
(4)外环自身有内凹的部分。外环轮廓有内凹部分时并不是所有情况都算作凹槽,如分别位于内凹轮廓两头的实体所构成的角度大于45°即不能算作凹槽处理,因为这样的内凹部分刀具是否可以深入加工决定于最小内R角半径值不受内凹部分的凹槽间距影响,图13(a)所示轮廓的内凹部分两头实体所构成角度为0,符合对凹槽的定义,槽间距取内凹部分两端点之间的绝对距离。图13(b)中轮廓的内凹部分两头的实体所构成角度a大于45°,不算作凹槽处理。
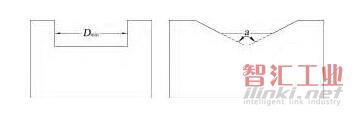
(a)作凹槽处理 (b)不作凹槽处理图13 外环自身内凹形成凹槽
2.3.2.2 凹槽的识别与槽间距的计算
依照凹槽的分类,不同类型的凹槽的识别方法也有差异的,下面针对不同类型的凹槽提出相应的识别方法。
(1)针对第一种环关系树零层的外环互相之间形成凹槽的类型,搜索构成轮廓的所有环,记录层值为0的环,两两求最小距离,综合比较这些距离,取最小值作为第一种类型凹槽的最小槽间距值。
(2)内环与其子环之间形成的间隙这一类型的凹槽的识别。利用图7所示的环关系树来具体说明,从上至下搜索奇数层的环,搜索到层数为1的环L3和L4,该环关系树除了第一层没有其他奇数层,环L3不存在子环,而环L4存在子环L5,则环L4与L5构成凹槽,求环L4与L5之间的最小距离,即为此类型凹槽的最小槽间距值。
(3)环关系树最高层的内环形成的凹槽。这种类型的凹槽识别需要借助环关系树,从下到上搜索奇数层环,并判断位于奇数层的环是否存在子环,若不存在则该环形成第三种类型的凹槽,由于内环的形状变化较多,难以归纳出一个精确确定槽间距的方法,因而作一些近似处理。图12所示为内环的3 种典型形状,图 12(a)内环形状为整圆或椭圆,槽间距为圆的直径或椭圆的短轴长度;图12(b)内环为矩形,槽间距为矩形短边的长度;图12(c)内环为三角形,槽间距为取3条边中最短边对应的中位线的长度。在分析第三种类型凹槽槽间距时将形成凹槽的内环简化成其如图12中的一种,然后求其槽间距值。
(4)外环自身内凹的部分形成的凹槽,这种类型凹槽的识别算法为:图14所示的轮廓方向为逆时针,其中ABCD这段轮廓构成整个环的内凹部分,A、B、C、D 4 个节点的凹凸性分别为凸、凹、凹、凸,由此可以得出规律,轮廓节点的凹凸性按照顺时针或者逆时针顺序排列,若存在凸+n*凹+凸(n≥2)这样的结构,则凸+n*凹+凸(n≥2)构成一个凹槽,识
别出组成凹槽的节点后,求2个凸节点之间的绝对距离,工程上将这个距离作为此类凹槽的槽间距,图14所示轮廓的槽间距即为A、D之间的绝对距离Dmin。
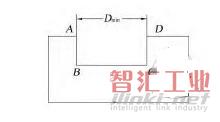
图14 外环自身内凹的凹槽的判断
3 应用实例
利用上述算法对图15所示的待加工电极模型的最小内R角和最小槽间距进行识别。
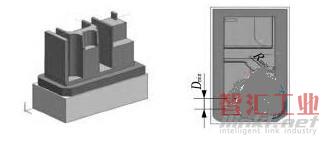
图15 待加工电极模型
(1)人工识别最小槽间距Dmin和最小内R角半径。经观察与手工测量,待加工电极最小槽间距Dmin=5.134 mm,最小内 R 角半径 Rmin=3.200 mm。
(2)使用上述介绍的算法编写的程序自动分析。
由图16(f)可以看到待加工零件共有5个台阶面,因而作5个截面,得到的截面轮廓见图16(a)~图16(e)。第 1 个截面轮廓图 16(a)是一个矩形,不存在内R角和槽间距;第2个截面轮廓如图16(b)所示:最小内R角半径值为R3.200mm,最小槽间距为5.134 mm;第 3、4、5 个截面轮廓的最小内 R 角半径值和槽间距值都在图中表示,可以看到取值与第2个轮廓一样。因而该零件的最小内R角半径值为R3.200 mm,最小槽间距值为 5.134 mm,对比人工识别的结果,完全一致。
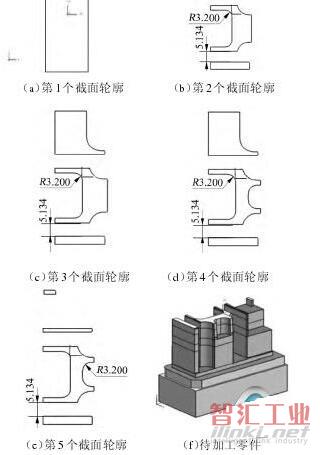
图16 半精加工特征识别实例
4 结束语
现有的数控加工自动编程系统往往需要工程师人为判断出零件是否需要半精加工,并指出所需加工刀具,是依赖人机交互的半自动编程。提出的半精加工特征识别算法,可极大提高数控自动编程系统的自动化程度,减少人机交互。经过某模具企业的大量实例验证,该算法针对电极的分析结果准确性高达80%,满足企业实际应用需求。
提出的算法先获取截面轮廓,然后对截面轮廓作几何分析从而获取所需参数以达到特征识别的目的。然而对截面轮廓所做的几何分析是一个复杂的过程,为了达到这个目的并简化实现过程,算法实现在多处作了工程近似处理。例如在识别轮廓的内R角半径时,对于一般样条曲线的凹凸性并不是单调的,最准确地获取最小内R角半径值的方法是将样条曲线分割成多条凹凸性单调的曲线,然后挑选出内凹的曲线段,最后求取这些内凹曲线段的最小半径值。然而将样条曲线分割成多条凹凸性单调的曲线的过程难度很大,暂时还没有理想的算法能够做到,因而作工程近似,所有样条曲线都按照等弧长等分成多条曲线段,并将每一条曲线段近似看作凹凸性是单调的,这个等弧长值设置的越小结果越接近实际情况,但是它设置太小导致等分数过多会影响计算效率,为了在效率与准确率之间找到平衡,必然需要牺牲一定的识别准确率。另外作截面轮廓时的精度以及几何分析时的精度设置都会影响识别准确率,由于研究时间有限,没能找到最理想的2个精确值,后续研究可以在这个方面作深入分析,找到更理想的精确值从而提高识别准确率。
(审核编辑: 智汇张瑜)