0 引言
我国独创的高速走丝电火花线切割机床,是目前使用的主要机种,但由于高速走丝线切割机床一般采用3B加工代码,使一般的图形化编程系统如UG,MasetrCAM无能为力。因此,高速走丝线切割机床的编程方式比较落后,主要采用手工编程,致使线切割的大部分功能得不到充分发挥,使用效率和效益都比较低。而图形交互式自动编程可以直接利用CAD模块生成的几何图形,采用人机交互的方式,自动进行必要的计算处理并编制出数控加工程序,具有速度快、精度高、直观性好、使用简便,以及对编程人员要求低等优点。因此,图形交互式自动编程是目前数控自动编程的首选方法。
1 设计基础理论
1.1 参数化理论
用AutoLISP语言进行二次开发的一个典型的、最重要的应用就是实现参数化绘图程序设计。参数化绘图是指几何图形拓扑关系不变,尺寸形状由一组参数进行约束,参数与图形的控制尺寸显示的对应,不同的参数值驱动产生不同大小的几何形状。
例如,图1所示的圆,首先按照通常的形状和拓扑约束关系定义几何模型;然后,根据圆的功能原理和设计要求定义尺寸参数;最后,分析得知该模型圆心O和直径D是其关键参数。只要改变圆心O的位置和直径D的大小,就会使得几何图形重构。参数化绘图理论在本设计中的应用,是通过提取实体属性表中的参数来约束加工轨迹的参数化模型,由此来推导加工轨迹中各特征点的计算关系,根据其具体的参数来约束加工轨迹的位置和大小。
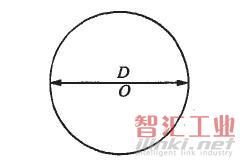
图1几何模型
1.2 3B程序的编写规则
1.2.1 程序格式
我国数控线切割机床采用统一的五指令3B程序,格式为: BxByBJGZ
其中:B——分隔符,用它来区分、隔离x,Y和J等数码,B后的数字若为0,则可省略不写;
x,y——直线的终点或圆弧起点的坐标值,编程时均取绝对值,μm;
J——计数长度,μm;
G——计数方向,分Gx或Gy,即可按菇方向或y方向计数,工作台在该方向每走1μm即计数累减1,当累减到计数长度J=0时,这段程序即加工完毕;
Z——加工指令,分为直线£和圆弧尺两大类。直线又按走向和终点所在象限分为L1,L2,L3,L44种(图2)。圆弧又按第一步进入的象限及走向的顺,逆圆而分为SRl,SR2,SR3,SR4,及NRl,NR2,NRt3,NR48种(图3)。
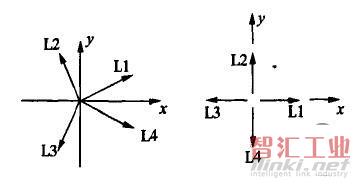
图2直线所在象限情况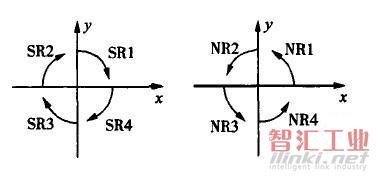
图3圆弧所在象限情况
1.2.2 直线的编程规则
1)把直线起点作为坐标的原点。
2)把直线的终点坐标值作为x,y,均取绝对值,单位为μm。
3)计数长度J,按计数方向Gx或Gy取该直线在x轴或Y轴上的投影值,以μm为单位,决定计数长度时,要和选计数方向一并考虑。
4)计数方向的选取原则,应取此程序最后一步的轴向为计数方向。不能预知时,一般选取与终点处的走向较平行的轴向作为计数方向,这样可减少编程误差和加工误差。对直线而言,取x,y中较大的绝对值和轴向作为计数长度J,和计数方向,具体可参照图4。
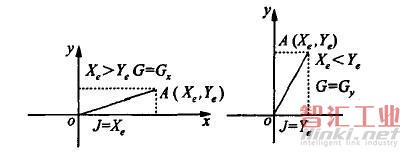
图4直线计数长度和方向判断
5)加工指令按直线走向和终点所在象限不同而分为L1,L2,13,L4,其中与+并轴重合的直线算作L1,与+y轴重合的直线算作L2,与一髫轴重合的直线算作L3,与-y轴重合的直线算作L4。具体可参考图2。与茹x,y轴重合的直线,编程时x,y均可作0,且在B后可不写。
注意:当x=y时,45°和225°取Gy,135°和315°取Gx。具体参照图5。
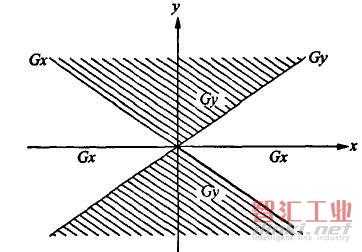
图5圆弧加工指令判断
1.2.3 圆弧的编程规则
1)把圆弧的圆心作为坐标原点;
2)把圆弧的起点坐标值作为x,y,均取绝对值,单位为μm;
3)计数长度J按计数方向取髫轴或Y轴上的投影值,以μm为单位。如圆弧较长,跨越两个以上象限,则分别取计数方向x轴(或y轴)上各个象限投影值的绝对值相累加,作为该方向的计数长度,也要和选计数方向一并考虑,如图6所示。
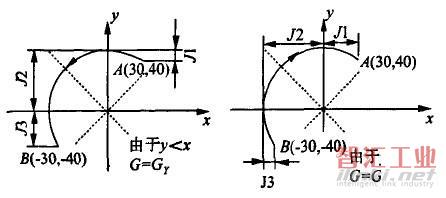
图6圆弧计数长度判断
4)计数方向同样也取与该圆弧终点走向较平行的轴向作为计数方向,以减少编程和加工误差。对圆弧来说,取终点坐标中绝对值较小的轴向作为计数方向(与直线相反),如图7所示。最好也取最后一步的轴向为计数方向。
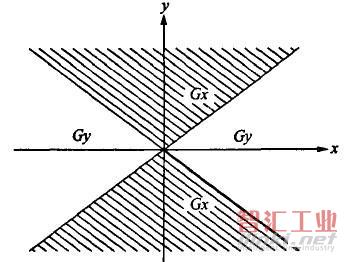
图7圆弧计数方向判断
5)加工指令对圆弧而言,按其第一步所进入的象限可分为R1,R2,R3,R4;按切割走向又可分为顺圆S和逆圆N,于是共有8种指令,即SR1,SR2,SR3,SR4;NR1,NR2,NR3,NR4,见图3所示。
注意:当起点位于坐标轴上时,顺圆和逆圆的加工指令是不一样的。具体也可参照图3。
1)若起点在x轴正方向上(即α=0°),则逆圆的加工指令为NR1,顺圆的加工指令为SR4。
2)若起点在y轴正方向上(即α=90°),则逆圆的加工指令为NR2,顺圆的加工指令为SRl。
3)若起点在茗轴负方向上(即α=180°),则逆圆弧的加工指令为NR3,顺圆的加工指令为SR2。
4)若起点在Y轴负方向上(即α=270°),则逆圆的加工指令为NR4,顺圆的加工指令为SR3。
1.3 加工轨迹的伪代码算法
1.3.1 伪代码算法概述
算法是解决“做什么”和“怎么做”的问题。做任何事情都有一定的步骤,这些步骤都是按一定的顺序进行的。广义的说,为解决一个问题而采取的方法和步骤,就称为“算法”。计算机算法可分为两大类数值运算算法和非数值运算算法。一个算法应该具有以下5个特点:1)有穷性;2)确定性;3)有零个或多个输入;4)有一个或多个输出;5)有效性。
1.3.2 3B指令生成伪代码算法
基于对线切割数控程序自动生成软件设计内容的理解,设计程序伪代码算法如下:

2 信息获取模块
要输出数控线切割3B程序,关键就是要编写出直线和圆弧3B程序自动生成的程序。而编写直线和圆弧的3B程序首先要解决的问题是直线和圆弧图形信息的获取。
2.1 直线3B程序模块
编写直线的3B程序,关键是要得到直线的起点和终点坐标,有了这两个参数后对特征点进行计算,根据其具体的参数来约束加工轨迹的位置和大小。最后,根据3B程序的书写格式,将数控程序以ASCII码的形式输出到文本文件中。设计直线3B程序流程图(图8)。
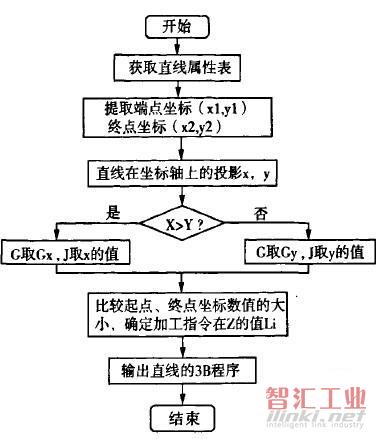
图8直线3B程序流程图
下面我们以一实例来具体介绍算法在程序设计中的运用。图9所示的一条直线,生成其3B程序的Auto LISP程序如下:

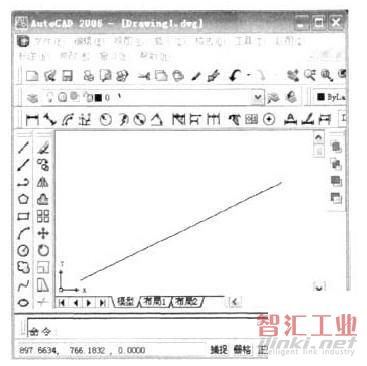
图9直线举例
有了直线的起点和终点坐标之后,通过计算直线在坐标轴上的投影,我们就可以得到3B编程五个参数中的髫,y值。其中要注意的是,AutoCAD中的绘图单位和编程单位在数值上相差1000,单位之间要进行转化。具体程序如下:

最终直线的3B程序为13622363 B288036 13622363Gx L1。
以上只是一条直线的例子,其余各种情况下直线线切割3B程序的编写,均可用上述方法获得。
2.3.2 圆弧3B程序模块
与直线相类似的,为了编写圆弧的3B程序,我们必须要知道圆弧的圆心、半径、起点、终点等相关参数,才能进行编程。设计圆弧3B程序自动生成的流程图如图10所示。

图10圆弧3B程序流程圈
下面,以典型实例来阐述算法在程序设计中的运用。如图11所示的圆弧,根据圆弧3B程序自动生成的流程图,编写LISP程序如下:

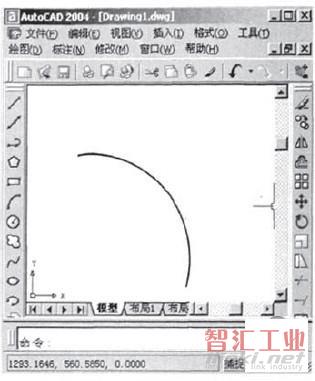
图11圆弧举例
最终圆弧的3B程序为B29484 13210842 B270757 Gy SR2。
以上只是第四象限的一条逆圆弧,其余各种情况下圆弧的数控线切割3B程序均可用以上方法来获得。
3 结语
综上可以看出,通过对于Lisp语言的运用,能够实现图形交互式自动编程,可以直接利用CAD模块生成的几何图形,采用人机交互的方式,自动进行必要的计算处理并编制出数控加工程序,提高了生产效率。但是如何对所编写的3B程序检验其正确性,也就是3B程序的仿真,是进一步研究的方向。
(审核编辑: 智汇小新)